Coding in junior mathematics
By: Steven Floyd and Lisa Anne Floyd
The Ontario Mathematics Curriculum for grades 1-8 includes one overall and two specific expectations related to coding, for each grade. In this article, the expectations from grades 4-6 are explored, in order to provide primary educators with potential insight and direction for implementation in their classroom.
The overall expectation, and specific expectations, are listed below:
C3. solve problems and create computational representations of mathematical situations using coding concepts and skills | ||
| Specific Expectations for Grade 4 C3.1 solve problems and create computational representations of mathematical situations by writing and executing code, including code that involves sequential, concurrent, repeating, and nested events C3.2 read and alter existing code, including code that involves sequential, concurrent, repeating, and nested events, and describe how changes to the code affect the outcomes | Specific Expectations for Grade 5 C3.1 solve problems and create computational representations of mathematical situations by writing and executing code, including code that involves conditional statements and other control structures C3.2 read and alter existing code, including code that involves conditional statements and other control structures, and describe how changes to the code affect the outcomes | Specific Expectations for Grade 6 C3.1 solve problems and create computational representations of mathematical situations by writing and executing efficient code, including code that involves conditional statements and other control structures C3.2 read and alter existing code, including code that involves conditional statements and other control structures, and describe how changes to the code affect the outcomes and the efficiency of the code |
What – What will students be doing?
The terms used in the curriculum expectations highlight the fact that students won’t simply be learning about coding, instead; students will be coding. This means that students will go beyond defining terms such as algorithm or variable, to the point where they are engaged in active learning through computing activities (Resnick & Rusk, 2020).
Expectation 3.2 indicates that students can read and alter code from existing programs, and then make predictions about how the changes to the code will affect the program output. In Expectation 3.1 students will write and execute their own programs. This emphasis on doing, rather than on learning about doing, provides students with the following three affordances:
- opportunities to make abstraction and other concepts tangible through code;
- opportunities to create their own dynamic models of mathematical concepts; and
- opportunities for student agency (Gadanidis, Brodie, Minniti & Silver, 2015).
How – How will students be doing it?
The curriculum expectations include the terms sequential, concurrent, and repeating, which can be thought of as ways that the code controls the events in a program (sometimes called control structures). These have been explored in a similar article for the primary grades.
What is new in grade 4, is the idea of nested events, which means that loops, for example, might appear inside of another loop, or nested within each other.
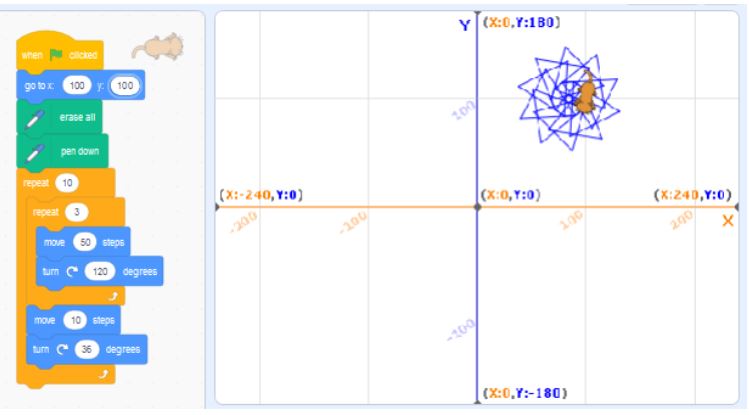
In grade 5, students will work with code that includes conditional statements, or decision-making structures. These are powerful components of coding that allow for the program to “make a decision”, or execute code only if a specific condition is met.
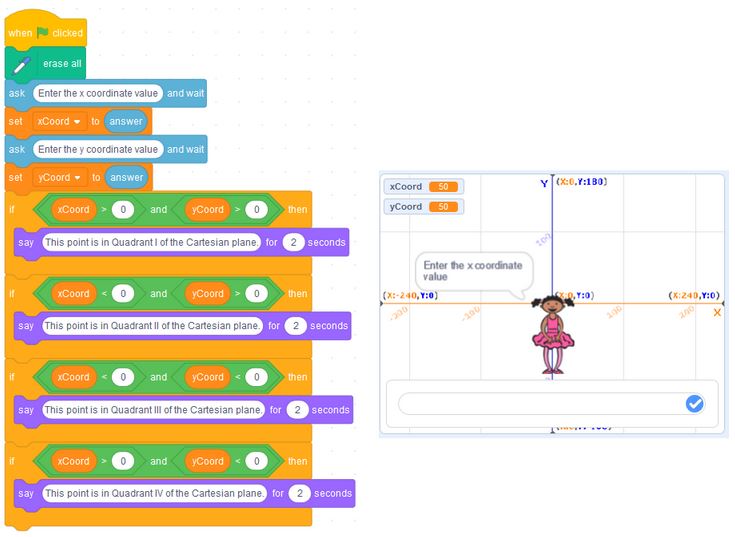
In grade 6, students will consider efficient code, which has value in terms of considering how to save time and storage space in programs and in general algorithms. Writing efficient code and algorithms also has an elegance and aesthetic value, that some teachers and students will certainly appreciate.
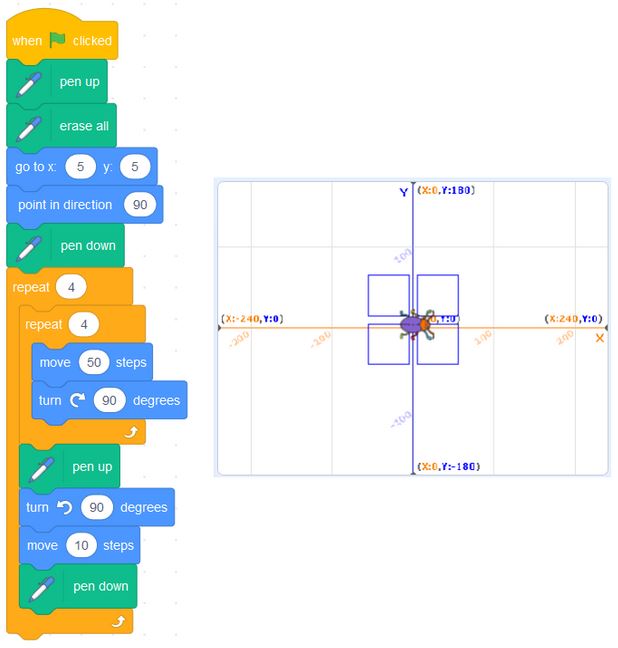
We’d suggest that it will be up to the teacher to interpret and decide which control structures will be used by students in each grade. Personal experience shows that grade 4 students can certainly program with conditional statements and consider coding efficiencies. We’d suggest that the power of coding may be best experienced by not limiting students to nested events in grade 4, and conditional events in grade 2.
Mathematical Context – What will they be learning as they do it?
The overarching theme of the curriculum expectations is for students to solve mathematical problems and create computational representations of mathematical situations. In this way, the context for the programs that students write can be selected from across any of the strands of the curriculum. This is highlighted in the curriculum context document, where it states “Coding can be incorporated across all strands and provides students with opportunities to apply and extend their math thinking, reasoning, and communicating.”
Within the junior grades, teachers may first find value in investigating the Geometric Reasoning and Location and Movement areas of Strand E – Spatial Sense for valuable coding contexts. The curriculum expectations in these areas lend themselves well to solving problems and creating computational representations with code as students experiment with geometric properties, Cartesian planes, and translations, reflections, and rotations.Potential expectation contexts for coding, from Strand E – Spatial Sense:
C3. solve problems and create computational representations of mathematical situations using coding concepts and skills | ||
| Specific Expectations for Grade 4 E1.1 identify geometric properties of rectangles, including the number of right angles, parallel and perpendicular sides, and lines of symmetry E1.2 plot and read coordinates in the first quadrant of a Cartesian plane, and describe the translations that move a point from one coordinate to another E1.3 describe and perform translations and reflections on a grid, and predict the results of these transformations E2.4 identify angles and classify them as right, straight, acute, or obtuse | Specific Expectations for Grade 5 E1.1 identify geometric properties of triangles, and construct different types of triangles when given side or angle measurements E1.4 plot and read coordinates in the first quadrant of a Cartesian plane using various scales, and describe the translations that move a point from one coordinate to another E1.5 describe and perform translations, reflections, and rotations up to 180° on a grid, and predict the results of these transformations E2.3 compare angles and determine their relative size by matching them and by measuring them using appropriate non-standard units | Specific Expectations for Grade 6 E1.1 create lists of geometric properties of various types of quadrilaterals, including the properties of the diagonals, rotational symmetry, and line symmetry E1.3 plot and read coordinates in all four quadrants of a Cartesian plane, and describe the translations that move a point from one coordinate to another E1.4 describe and perform combinations of translations, reflections, and rotations up to 360° on a grid, and predict the results of these transformations E2.2 use a protractor to measure and construct angles up to 360°, and state the relationship between angles that are measured clockwise and those that are measured counter-clockwise |
References:
Gadanidis, G., Brodie, I., Minniti, L., & Silver, B. (2017). Computer Coding in the K-8 Mathematics Curriculum. What Works: Research Into Practice.
Resnick, M., & Rusk, N. (2020). Coding at a crossroads. Communications of the ACM, 63(11), 120-127.