Coding in intermediate mathematics
By: Steven Floyd and Lisa Anne Floyd
The Ontario Mathematics Curriculum for grades 1-8 includes one overall and two specific expectations related to coding, for each grade. In this article, the expectations from grades 7-8 are explored, in order to provide primary educators with potential insight and direction for implementation in their classroom.
The overall expectation, and specific expectations, are listed below:
C3. solve problems and create computational representations of mathematical situations using coding concepts and skills | |
| Specific Expectations for Grade 7 C3.1 solve problems and create computational representations of mathematical situations by writing and executing efficient code, including code that involves events influenced by a defined count and/or sub-program and other control structures C3.2 read and alter existing code, including code that involves events influenced by a defined count and/or sub-program and other control structures, and describe how changes to the code affect the outcomes and the efficiency of the code | Specific Expectations for Grade 5 C3.1 solve problems and create computational representations of mathematical situations by writing and executing code, including code that involves the analysis of data in order to inform and communicate decisions C3.2 read and alter existing code involving the analysis of data in order to inform and communicate decisions, and describe how changes to the code affect the outcomes and the efficiency of the code |
What – What will students be doing?
The terms used in the curriculum expectations highlight the fact that students won’t simply be learning about coding, instead; students will be coding. This means that students will go beyond defining terms such as algorithm or variable, to the point where they are engaged in active learning through computing activities (Resnick & Rusk, 2020).
Expectation 3.2 indicates that students can read and alter code from existing programs, and then make predictions about how the changes to the code will affect the program output. In Expectation 3.1 students will write and execute their own programs. This emphasis on doing, rather than on learning about doing, provides students with the following three affordances:
- opportunities to make abstraction and other concepts tangible through code;
- opportunities to create their own dynamic models of mathematical concepts; and
- opportunities for student agency (Gadanidis, Brodie, Minniti & Silver, 2015).
How – How will students be doing it?
The curriculum expectations include the concept of efficiency of code, which has been explored in a similar article for the junior grades.
What is new in grade 7, is the idea of a subprogram, which is sort of like a mini program that can be used by the main program anytime it needs it. As an example, a student might write code for a subprogram that draws a square, then anytime they need to draw a square they can simply call the subprogram from their main program, and a square is drawn.
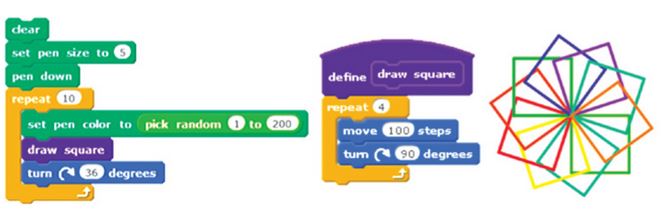
Creating subprograms in coding projects can help make code more efficient, since subprograms can be reused many times in the main program. They also tie very closely to the concept of abstraction, which is a powerful idea related to Computational Thinking. This idea is explored in depth in Computer Coding in the K–8 Mathematics Curriculum? by Gadanidis, Brodie, Minniti & Silver (2017).
In grade 8, students will work with code in an effort to use data to make decisions. This is a powerful idea that can truly bring home to students the power of computing. Students can run simulations on large sets of data, or scan through data to find the largest or smallest values and make decisions based on this information. The idea of using data to make decisions also connects well to very timely computing concepts such as big data, bias in data, artificial intelligence and machine learning.
We’d suggest that it will be up to the teacher to interpret and decide which concepts will be used by students in each grade. Personal experience shows that grade 7 students can certainly program with data to make decisions. We’d suggest that the power of coding may be best experienced by not limiting students to exploring coding and data only in grade 8.
Mathematical Context – What will they be learning as they do it?
The overarching theme of the curriculum expectations is for students to solve mathematical problems and create computational representations of mathematical situations. In this way, the context for the programs that students write can be selected from across any of the strands of the curriculum. This is highlighted in the curriculum context document, where it states: “Coding can be incorporated across all strands and provides students with opportunities to apply and extend their math thinking, reasoning, and communicating.”
Within the intermediate grades, teachers may first find value in Strand D – Data and Strand E – Spatial Sense for valuable coding contexts. The curriculum expectations in these areas lend themselves well to solving problems and creating computational representations with code as students experiment with subprograms and data.
Potential expectation contexts for coding, from Strand E – Spatial Sense:
C3. solve problems and create computational representations of mathematical situations using coding concepts and skills | |
| Specific Expectations for Grade 7 D1.2 collect qualitative data and discrete and continuous quantitative data to answer questions of interest, and organize the sets of data as appropriate, including using percentages E1.1 describe and classify cylinders, pyramids, and prisms according to their geometric properties, including plane and rotational symmetry E1.3 perform dilations and describe the similarity between the image and the original shape E1.4 describe and perform translations, reflections, and rotations on a Cartesian plane, and predict the results of these transformations | Specific Expectations for Grade 8 D1.1 identify situations involving one-variable data and situations involving two-variable data, and explain when each type of data is needed D1.2 collect continuous data to answer questions of interest involving two variables, and organize the data sets as appropriate in a table of values D2.1 solve various problems that involve probability, using appropriate tools and strategies, including Venn and tree diagrams E1.1 identify geometric properties of tessellating shapes and identify the transformations that occur in the tessellations E1.4 describe and perform translations, reflections, rotations, and dilations on a Cartesian plane, and predict the results of these transformations |
References:
Gadanidis, G., Brodie, I., Minniti, L., & Silver, B. (2017). Computer Coding in the K-8 Mathematics Curriculum. What Works: Research Into Practice.
Resnick, M., & Rusk, N. (2020). Coding at a crossroads. Communications of the ACM, 63(11), 120-127.