By: Lisa Anne Floyd and Steven Floyd
Note: There are three other resources that support this learning:
Student activity page – Teacher solutions page – Student solutions page
In high school computer science classes around Ontario, students make regular use of a for loop that repeats code. This for loop allows students to create patterns of numbers or to execute code a certain number of times in order to complete a task. Now that coding is part of the grade 9 mathematics curriculum in Ontario, for loops can also be an excellent tool to explore and represent algebraic expressions.
In this resource, we will explore an approach to teach about algebraic expressions and tables of values by coding using the Python programming language.
Check out this related webinar that was recorded on Tuesday, February 15th, 2022, and facilitated by Lisa Anne and Steven.
Algebraic Reasoning
First, let’s take a brief look at an overview of Algebraic Reasoning. You may want to check out this Ontario Principals’ Council webinar led by Dr. Ruth Beatty, which provides a comprehensive explanation about developing algebraic thinking in young minds.
Let’s start by looking at some simple growing patterns…
Consider the following lists of numbers,- what is the missing value in each of the lists?
2, 4, 6, ? 3, 6, 9, ?
At a very young age, children are able to come up with the next number. They tend to readily use recursive reasoning in the process. Here, they are determining the fourth term by using addition – they are able to extrapolate to determine what comes next.
But, what if we want to know the 10th or 100th term value?
Recursive reasoning, which is what was used here, is no longer as helpful. Many students’ first instinct, even in grade 9, is to think recursively or to perform addition, likely because of their experiences with skip counting in younger grades.
Ideally, we want to help set the stage for students to make use of algebraic reasoning so that it becomes more natural for them to determine term values. Let’s look at some simple growing patterns from a different perspective…
We will now begin with two sets of values, and focus on the relationship between the two sets of values, rather than what comes next.
You might phrase a question like this:
What do you have to do to the numbers in the left column to get the numbers in the right column?
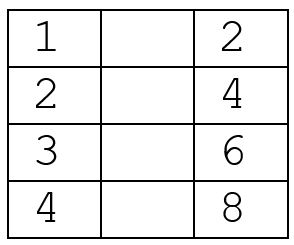
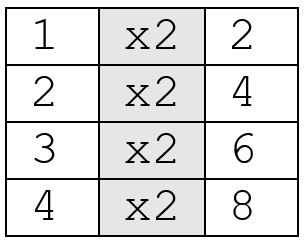
Students will notice that they have to multiply the numbers in the column on the left by 2 to get the numbers in the column on the right:
Here’s another set of values that might be given to students:
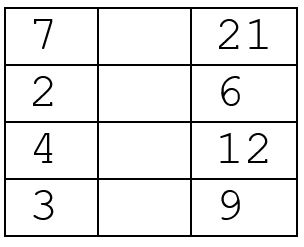
By providing sets of data that aren’t in numerical order, we can focus on looking at the relationship between two sets of data so students can’t look ahead and easily predict the next number in the pattern.
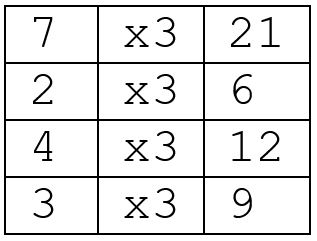
You will notice that we had to multiply the numbers on the left by 3 to get the numbers on the right:
To encourage students to use this type of explicit or functional reasoning, you might have observed primary school teachers playing the “robot” game, in which students input a value into the “robot”. The “robot” will then perform a function and spit out the new value. The students’ job is to determine what function the “robot” is applying to the values.
Example:

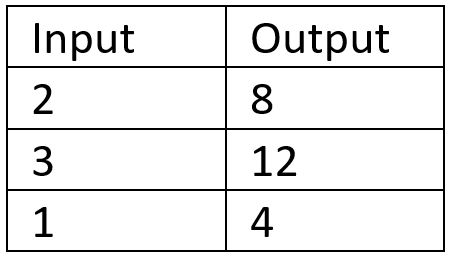
Students will figure out that the robot is multiplying each inputted value by 4!
Now that we’ve looked at an approach often used as an introduction to algebraic reasoning, let’s explore how we can incorporate coding to support this type of thinking.
Exploring Mathematics through Coding
To explore algebraic expressions, we will alter or “tinker” with code. Tinkering involves taking “things apart, and engaging in changes and/or modifications to existing objects” (Kotsopoulos et al., 2017). Tinkering has direct connections to curriculum expectations in grade 9 Mathematics, and in grades 1-8 as well, as students are expected to read and alter code.
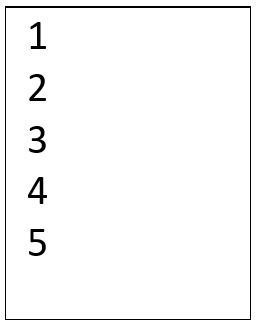
We will write a few lines of code in Python that make use of a repeat called a “for loop” to generate tables of values for various expressions. Similar code can be written in any programming language. Here are what for loops look like in a few different languages. Each of these examples will output the numbers 1 through 5 on the screen. Don’t worry – we will discuss how for loops work in a moment.
Table: For loops in various programming languages.

Each of these programs will output the following:
As mentioned, the lines of code we will write are typically seen in a computer science classroom in high school. Students learn how to alter the range and variable values in their for loops to produce the desired output. In this case, we will be applying this skill to explore mathematics concepts.
These lines of code are the basis with what students will be tinkering. We can tinker with this code to create various representations of algebraic expressions.
This approach affords students to use the grade 9 coding expectations (shown below) in the curriculum to access and work with other mathematics expectations in grade 9.
C2.1 use coding to demonstrate an understanding of algebraic concepts including variables, parameters, equations, and inequalities
C2.2 create code by decomposing situations into computational steps in order to represent mathematical concepts and relationships, and to solve problems
C2.3 read code to predict its outcome, and alter code to adjust constraints, parameters, and outcomes to represent a similar or new mathematical situation
Check-out this PRIMM pedagogical framework we previously shared that might be incorporated when teaching about coding.
Python and Algebraic Expressions – Try It!
Let’s explore algebraic expressions through Python ourselves!
Follow along with this activity below to explore one way to connect math with coding.
1 – Go to the following website and type the code into this Console as shown.
https://cscircles.cemc.uwaterloo.ca/console/
*You can also use Google Colab if your school board has access
Keep in mind that in coding, words are case sensitive, symbols must be exact, and indentation is important. Don’t worry – you’ll get used to this if coding is new to you!
The backwards slash (“\”) can usually be found above the enter key on your keyboard.
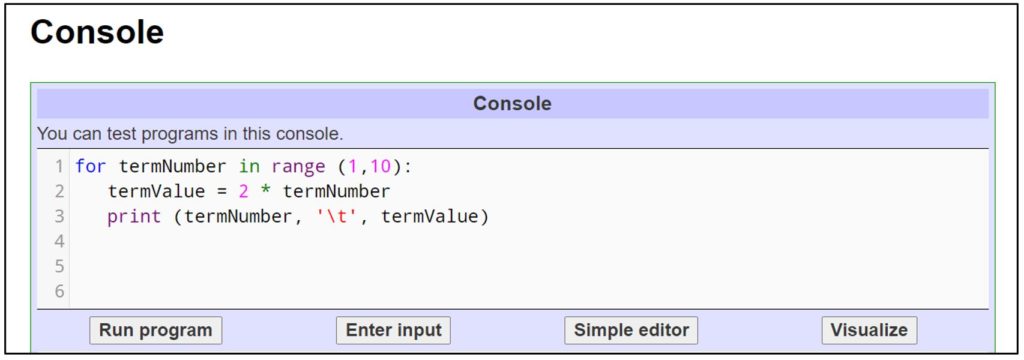
Code:
for termNumber in range (1,10):
termValue = 2 * termNumber
print (termNumber, ‘\t’, termValue)
Here’s what it looks like when we’ve typed the code into the console:
2 – Click on Run program.
Your output should look like this:
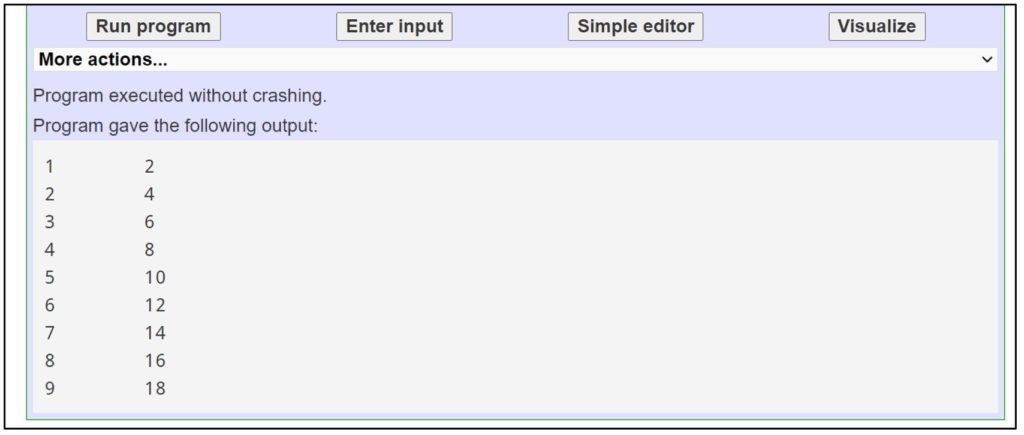
Often, when we are coding, we will get an error message. This error message helps us to determine which line of code contains an error. Typically, people might leave out a colon or spell a variable name wrong. Double-check that you’ve typed everything correctly and click on Run program again.
Let’s try to understand what’s happening with our code.
First, let’s look at the math equation in our code.
The equation that is being shown in our table of values is:
y = 2x Note: In our code, we’ve written it like this: termValue = 2 * termNumber
- x represents the term number and
- y represents the term value
In programming, we tend to use variable names that are more descriptive – this helps us to understand what is happening in the code. You can replace the variable names with y and x if you prefer.
If we were to create a representation using tiles, which we often see in resources related to patterning, it might look something like this for the expression 2n:
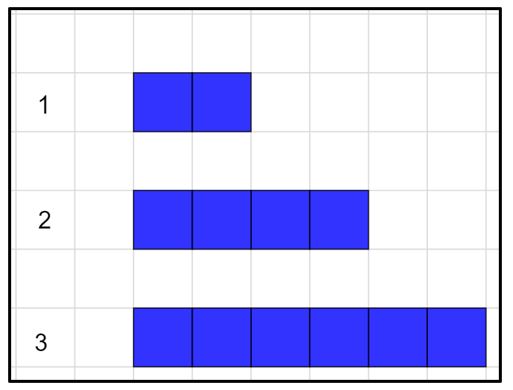
Note: We used this Colour Tiles app from Mathies to generate these virtual tiles.
Rather than tiles, we are creating a representation of a table of values using coding as our tool.
Explaining the Code
Now, let’s look at the code in more detail.

The word “for” indicates the start of a loop. This for loop will be executed 9 times, beginning at 1 and ending at 9. In Python, the 10 means that we go up to, but not including 10.
How can you alter the code so that term numbers 1 to 10 are displayed rather than just 1 to 9?
Scroll down for the answer…
ANSWER –

Now when you run the code, the termNumber variable will start at 1 and go up to, but not including 11.
Try This: Adjust the code now so that it will output 100 rows of numbers.
Did it work on your first try? It usually takes us a few tries to get things working when we are coding. It is great to model this for our students, so don’t worry if you make a few mistakes while demonstrating how to create representations with Python code.
Let’s continue to explore the code…
termNumber is a variable – that means it contains a value that varies!
There is one other variable in the program we’ve written. What is it called?
ANSWER – termValue
What does the asterisk (*) mean when we are coding?
ANSWER – to multiply!
What does the \t do in Python?
ANSWER – it inserts a tab for spacing
The code that is indented beneath the for loop means that it is inside of the loop. This code will repeat a total of 9 times if the range is (1,10) and ten times if the range is (1,11).
Let’s read through the original code using our own words – a natural language (students could also be challenged to do this, to express what each line of code does in simple language):
Begin loop, the first time through the loop, termNumber will be 1.
Multiply the termNumber by 2 and store it in the variable termValue (termValue is now 2)
Print the current value of termNumber, insert a tab, print the current value of termValue
Loop again… termNumber now has a value of 2.
Multiply the termNumber by 2 and store it in the variable termValue (termValue is now 4)
Print the current value of termNumber, insert a tab, print the current value of termValue
Loop again… termNumber now has a value of 3.
Multiply the termNumber by 2 and store it in the variable termValue (termValue is now 6)
Print the current value of termNumber, insert a tab, print the current value of termValue
…
…
…
Repeat this until termNumber has the last value (up to but no including the 10).
Try this: Alter the code so that the following output is displayed when the code is executed.

Scroll down for the answer.
ANSWER –

Representing Algebraic Expressions with Tables of Values in Python
Practice! Alter the code to create the output shown. Check out our solutions if you are stuck.
1 –

2 –
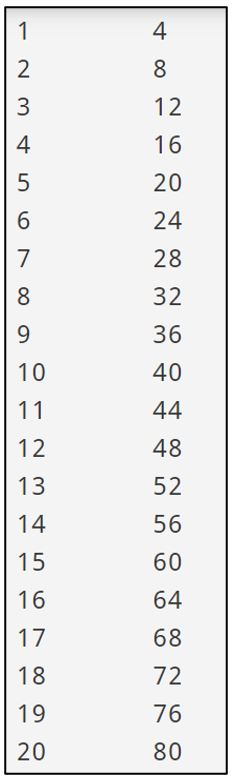
3 –
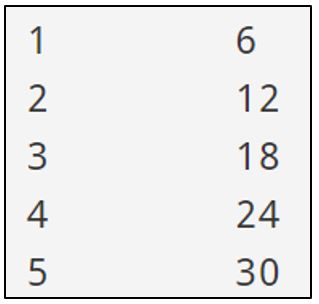
4 –
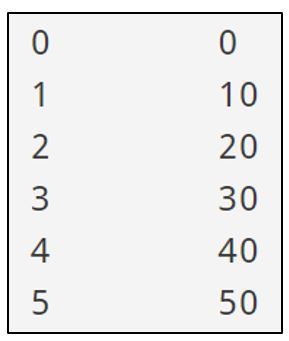
5 – (nonlinear)

Incorporating Constants
Try This: Look at the following code. Predict what the output will be when the code is executed (predicting the outcome of code is part of expectation C2.3).

ANSWER –
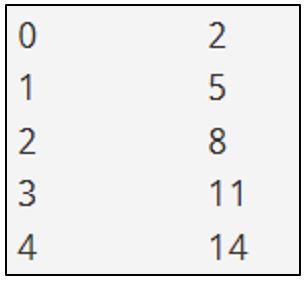
As you can see here, we’ve introduced a constant to our expression. Encouraging students to show the output when the termNumber is 0, helps them to determine the value of the constant.
You might also introduce two additional variables and alter the code like this:

Practice! Alter the code to create the output shown. Check out our solutions if you are stuck.
1 –

2 –

More Practice! Predict what will be outputted when the code is executed. If you are not sure, try typing the code in the console and run the program to check if you were right .
1 –

2 –

Next Steps:
- Check out this Student Activity with guided materials and practice questions for students to try. The solutions for this student activity are also provided.
- Have students come up with their own tables of values through coding in Python. They can challenge one another to recreate the tables of values by writing the code and comparing their approaches. You’ll find they’ll naturally start incorporating negative numbers, real numbers, and nonlinear expressions to stump one another (and you!).
- As an alternative, you might have on hand a collection of cards that contain tables of values for students to reproduce using code – you can have varying degrees of challenges on the cards for differentiation, and hand them out based on student readiness.
Incrementing the Term Number by Values Other than 1
Once students start using the code to write several tables of values, they might wish to increment the Term Number by larger values.
Let’s look at a real-life example to explore this concept.
Farrah looks into renting a hall for her family to gather when her sister is visiting from British Columbia. The hall charges a flat rate of $500 and an additional $25 per person.
In this case, the multiplier is $25 and the constant is $500. The expression is 25n + 500.
The code for the expression would be termValue = 25 * termNumber + 50
Here is a table of values that represents the expression for this scenario.
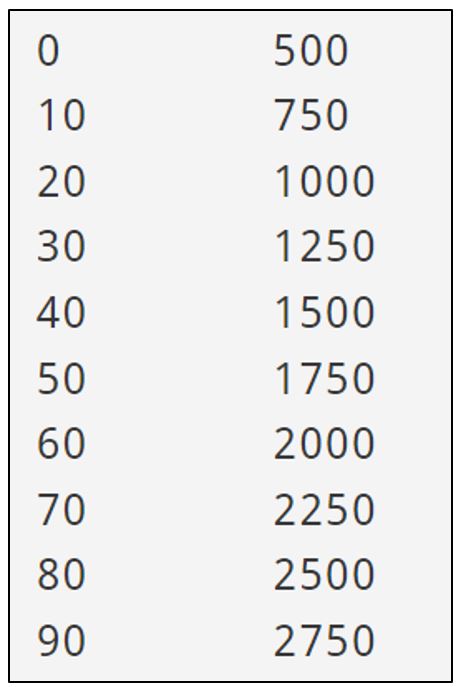
Notice the Term Number is going up by 10.
Here is the code to produce this particular table of values:

Notice the range has been adjusted – we have used (0,100,10) – the 10 represents by which value the variable termNumber will increase. We’ve also incorporated descriptive names for the variables.
Students might also wish to add headings for their table of values:

The output with headings looks like this:
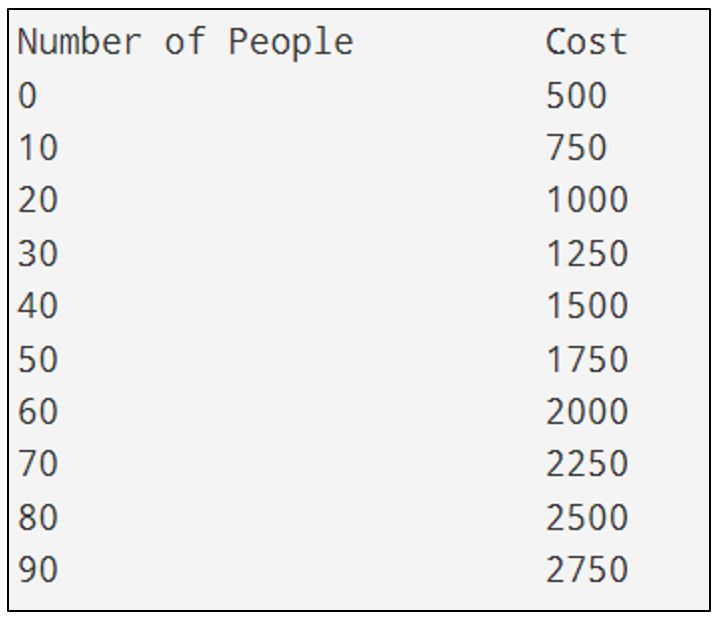
Try This: Alter the code so that the termNumber goes up by 5.
Writing Expressions for Real-Life Applications
Practice! Write code that will output a table of values to represent the following scenarios. Check out our solutions if you are stuck.
1 – Hanaa gets reimbursed $0.45 for her kilometers when she volunteers to deliver meals to the community. Write code that will generate a chart to show the amount she will be paid up to and including 100 km.
2- Immaculate gets paid a flat rate of $10 and $0.30 per flyer she delivers in her neighbourhood. Write code that will generate a chart to show the amount she will be paid up to 50 flyers.
3 – A vehicle has a purchase price of $24 500. Each year, its value depreciates an average of $1500. Write code to generate a chart that will show the value of the car in comparison to the number of years owned over the course of 5 years.
4 – A backyard pond contains 300 gallons of water. It loses about 5 gallons of water per day due to evaporation. Write code to generate a chart that will show the capacity of the pond in gallons over the course of 7 days.
5 – (Exponential Growth) The population of a city at the beginning of 2022 was 10 000 people. It was noticed that the population of the city grows at a steady rate of 5 % annually. Write code to show the projected population size for the next 10 years.
Want more practice questions? Check out TVO Mathify – there are questions for the new grade 9 math curriculum that you can open on a whiteboard.
Note: You will need to log in using your school board email address and then go to this link to access the question bank.
Help us to improve!
Let us know if you have any suggestions for improvement or corrections on our resources.